simetria

La simetría es un rasgo característico de formas geométricas, sistema, ecuaciones, y otros objetos materiales o entidades abstractas.

En condiciones formales, decimos que un objeto es simétrico en lo que concierne a una operación matemática dada, si, cuando aplicado al objeto, esta operación no cambia el objeto o su aspecto. Dos objetos son simétricos uno al otro en lo que concierne a un grupo dado de operaciones si uno es obtenido de otro por algunas operaciones (y viceversa). En la geometría 2D las clases principales de simetría de interés son las que conciernen a las isometrías de un espacio euclídeo: traslaciones, rotaciones, reflexiones y reflexiones que se deslizan.

La simetría también puede ser encontrado en organismos vivos.

Simetría en geometría

Grupo de simetría de la esfera.

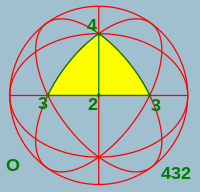
Cuando hablamos de objetos físicos o elementos geométricos el concepto de simetría está asociado a transformaciones geométricas tales como las rotaciones, las reflexiones o las traslaciones. Así se dice que un objeto presenta:

• Simetría esférica si existe simetría bajo cualquier rotación posible, matemáticamente equivale a que el grupo de simetría de un objeto físico o entidad matemática sea SO(3).
• Simetría cilíndrica o axial, si existe un eje tal que los giros alrededor de él no conducen a cambios de posición en el espacio, matemáticamente está asociado a un grupo de isometría SO(2).
• Simetría reflectiva,se define por la existencia de un único plano, matemáticamente está asociado al grupo SO(1) o su representación equivalente .

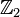Si tratamos además de regiones geométricas infinitas, no acotadas, además puede existir simetría traslacional. Todas estas simetrías posibles son además isometrías.

Simetría en física

En física el concepto de simetría puede formularse en una forma no geométrica. Si K es un conjunto de objetos matemáticos del mismo tipo (funciones, formas geométricas, ecuaciones, ...) y G es un grupo de transformaciones que actúa sobre K de tal manera que:

Se dice que un elemento de k₀ presenta simetría si:^[1]

Así por ejemplo varias leyes de conservación de la física son consecuencia de la existencia de simetrías abstractas del lagrangiano, tal como muestra el teorema de Noether. En ese caso K representaría el conjunto de lagrangianos admisibles, k₀ el lagrangiano del sistema bajo estudio y G puede representar traslaciones espaciales (conservación del momento lineal), traslaciones temporales (conservación de la energía), rotaciones (conservación del momento angular) u otro tipo de simetrías abstractas (conservación de la carga eléctrica, el número leptónico, la paridad, etc.).

• Ejemplo 1. Como primer ejemplo consideremos un electrón moviéndose entre dos placas infinitas cargadas uniformemente (dicho sistema se aproxima cierto tipo de condesadores), dado que cualquier tralación paralela a los planos constituye una simetría del sistema físico, entonces tanto la fuerza paralela a dichos planos es nula y por tanto la velocidad paralela a los planos es constante.

• Ejemplo 2. Consideremos un satélite orbitando alredodor de un astro (planeta o estrella) con simetría esférica perfecta, consideremos además que la velocidad del satelite sea perpendicular a la línea entre el centro del satélite y el astro. En ese caso, el lagrangiano es totalmente invariante respecte a rotaciones según un eje que pase por el centro de la fuente del campo gravitatorio. En este caso debido a la simetría de rotación tanto del lagrangiano como de las condiciones iniciales del movimiento, la velocidad perpendicular al planeta es constante y la trayectoria es un círculo invariante bajo una rotación perpendicular al plano de la órbita.

Estos dos ejemplos anteriores son casos del teorema de Noether, un resultado general que establece que si existe un grupo uniparamétrico de simetría G para el lagrangiano tal que:

Entonces la cantidad escalar:

Siendo v el campo vectorial que general el grupo uniparamétrico de transformaciones de simetría, y p_i los momentos conjungados de las coordenadas generalizadas de posición.